This is an excerpt from the Ralph E. Davis Associates (RED) Weekly E&P Update Newsletter.

If you Google the phrase “terminal decline,” you’re likely to get a lot of unpleasant results about the rapid loss of cognitive function immediately preceding death. Let’s start by clarifying that’s not what we’re talking about. In reservoir engineering, terminal decline is a concept applied in decline curve analysis to describe the (typically) late-life production rate behavior of oil and gas wells.

In 1944, J.J. Arps published what’s now called the Arps Equation to describe and predict the production rate behavior of a producing well under constant bottomhole flowing pressure. It was derived from empirical observations of oil wells under certain conditions but has been found to have wide applicability to many depletion drive reservoirs, particularly “tight” and unconventional formations.

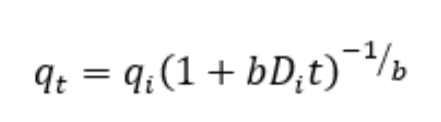
Arps Equation

The ”b” term in the equation, called the “hyperbolic exponent” or the “b-factor,” is a dimensionless term that causes the decline curve to flatten over time. In the Arps equation, “b” is assumed to be constant over the life of the well, but it actually gets smaller over time as the well moves through different flow regimes. The effect of the constant b-factor assumption is for the decline rate to continually go down, and eventually, the well is forecast to produce at a nearly constant rate. This may result in a large overestimate of ultimate recovery, however.

To prevent this type of behavior, most engineers assume that the “hyperbolic” behavior predicted by the Arps equation switches to constant exponential decline (b=0) once the well reaches a particular decline rate, called the “terminal decline” or “Dmin”. For example, once the well reaches a 6% decline, the decline rate no longer flattens. In the SPEE’s 2021 Annual Parameters Survey, over 90% of the respondents said they always or usually use the Arps equation for production forecasting and most of them switch to exponential decline with an assumed terminal decline rate of 4%-7%.

Despite its wide usage, there are some pitfalls to the use of a terminal decline. It can’t be derived analytically in real-world situations, so if it occurs, it must be observed. That’s a problem where there aren’t wells with sufficient production history to exhibit a terminal decline. There’s no physical reason why wells must switch from hyperbolic to exponential decline, and some wells may not. Many researchers point out that it’s more accurate to create production forecasts with multiple segments using different (declining) b-factors, and that the final segment’s b-factor may lie in the 0.3 to 0.5 range. The challenge with this approach is the additional time required to identify flow regimes, determine the decline parameters and build the forecasts. Identifying the flow regimes also requires enough production history (often in offset wells) to have observed them.

For economic purposes, the assumed value of the terminal decline typically has a small impact on the present value of future reserves. And as wells get older, new forecasts will be generated that use the most recent production behavior and may indicate a low, but non-zero b-factor, eliminating the need for a terminal decline assumption.

About the Author:

Steve Hendrickson is the president of Ralph E. Davis Associates, an Opportune LLP company. Hendrickson has over 30 years of professional leadership experience in the energy industry with a proven track record of adding value through acquisitions, development and operations. In addition, he possesses extensive knowledge of petroleum economics, energy finance, reserves reporting and data management, and has deep expertise in reservoir engineering, production engineering and technical evaluations. Hendrickson is a licensed professional engineer in the state of Texas and holds an M.S. in Finance from the University of Houston and a B.S. in Chemical Engineering from The University of Texas at Austin. He recently served as a board member of the Society of Petroleum Evaluation Engineers and is a registered FINRA representative.

Comments